When dealing with univariate data you want to do one or more of
- Find a good model for the data.
- Estimate parameters for your candidate models.
- Get an idea about the uncertainty of your estimates.
The unvariateML package has a fast and reliable
functions to help you with these tasks. The core of the package are more
than 20 functions for fast and thoroughly tested calculation of maximum
likelihood estimates for univariate models.
- Compare the fit of your candidate models with
AICorBIC. - Look at QQ plots or PP plots of your data.
- Plot the data together with density estimates.
- Compute confidence intervals using parametric bootstrap.
This vignette shows you how to use the tools of
univariateML to do exploratory data analysis.
Mortality in Ancient Egypt
The dataset egypt contains contains the age at death of
141 Roman era Egyptian mummies. Our first task is to find a univariate
model that fits this data.
library("univariateML")
head(egypt)## age sex
## 1 1.50 male
## 2 1.83 male
## 3 2.00 male
## 4 2.00 male
## 5 3.00 male
## 6 3.00 male
hist(egypt$age, main = "Mortality in Ancient Egypt", freq = FALSE)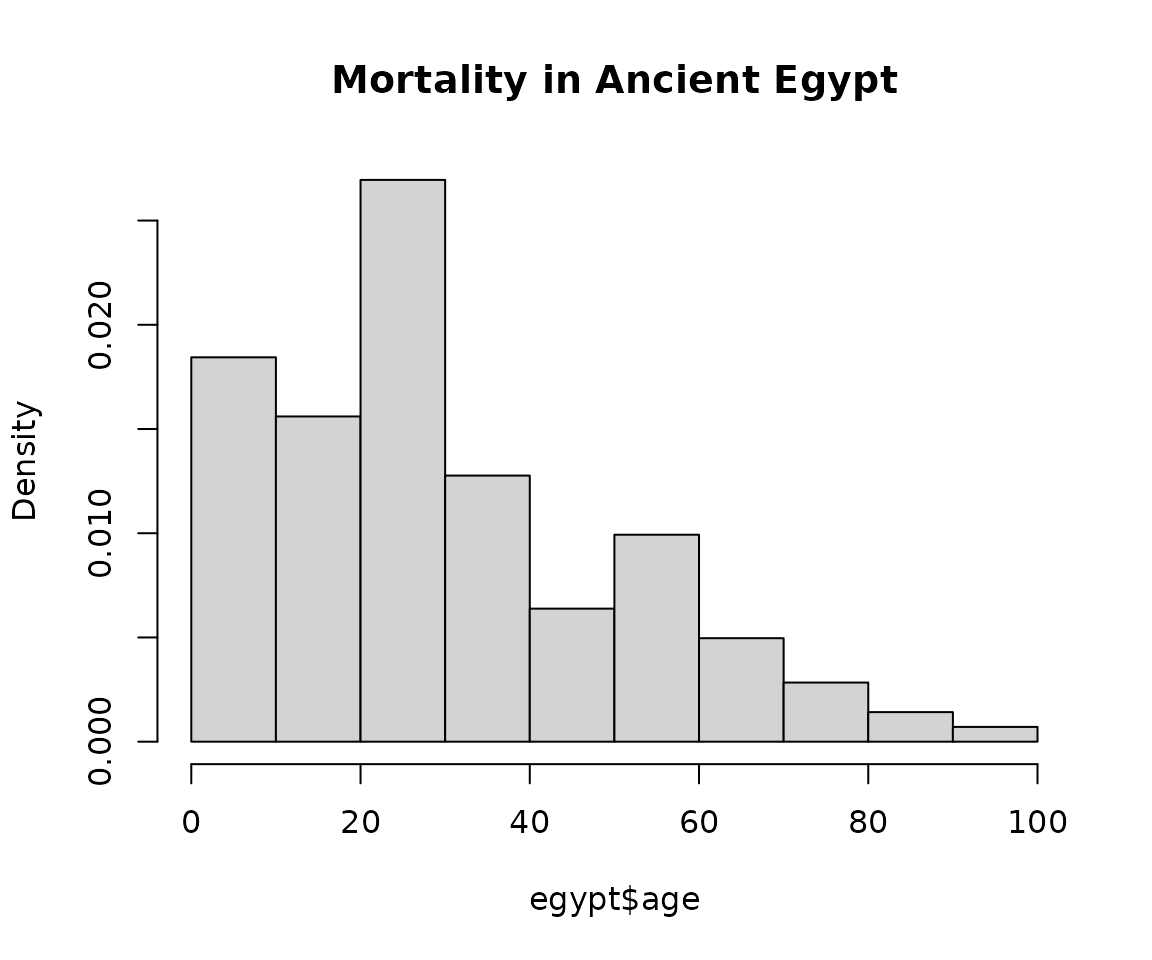
Comparing Many Models with AIC
The AIC
is a handy and easy to use model selection tool, as it only depends on
the log-likelihood and number of parameters of the models. The generic
in R can take multiple models, and the lower the the
better.
Since all the data is positive we will only try densities support on the positive half-line.
AIC(
mlbetapr(egypt$age),
mlexp(egypt$age),
mlinvgamma(egypt$age),
mlgamma(egypt$age),
mllnorm(egypt$age),
mlrayleigh(egypt$age),
mlinvgauss(egypt$age),
mlweibull(egypt$age),
mlinvweibull(egypt$age),
mllgamma(egypt$age)
)## Loading required package: intervals## df AIC
## mlbetapr(egypt$age) 2 1312.464
## mlexp(egypt$age) 1 1249.553
## mlinvgamma(egypt$age) 2 1322.949
## mlgamma(egypt$age) 2 1234.772
## mllnorm(egypt$age) 2 1263.874
## mlrayleigh(egypt$age) 1 1260.217
## mlinvgauss(egypt$age) 2 1287.124
## mlweibull(egypt$age) 2 1230.229
## mlinvweibull(egypt$age) 2 1319.120
## mllgamma(egypt$age) 2 1314.187The Weibull and Gamma models stand out with an AIC far below the other candidate models.
To see the parameter estimates of mlweibull(egypt$age)
just print it:
mlweibull(egypt$age)## Maximum likelihood estimates for the Weibull model
## shape scale
## 1.404 33.564mlweibull(egypt$age) is a univariateML
object. For more details about it call summary:
##
## Maximum likelihood for the Weibull model
##
## Call: mlweibull(x = egypt$age)
##
## Estimates:
## shape scale
## 1.404158 33.563564
##
## Data: egypt$age (141 obs.)
## Support: (0, Inf)
## Density: stats::dweibull
## Log-likelihood: -613.1144Automatically select the best model
The model selection process can be automatized with
model_select(egypt$age):
model_select(egypt$age, models = c("gamma", "weibull"))## Maximum likelihood estimates for the Weibull model
## shape scale
## 1.404 33.564Quantile-quantile Plots
Now we will investigate how the two models differ with quantile-quantile plots, or Q-Q plots for short.
qqmlplot(egypt$age, mlweibull, datax = TRUE, main = "QQ Plot for Ancient Egypt")
# Can also use qqmlplot(mlweibull(egypt$age), datax = TRUE) directly.
qqmlpoints(egypt$age, mlgamma, datax = TRUE, col = "red")
qqmlline(egypt$age, mlweibull, datax = TRUE)
qqmlline(egypt$age, mlgamma, datax = TRUE, col = "red")
The Q-Q plot shows that neither Weibull nor Gamma fits the data very well.
If you prefer P-P plots to Q-Q plots take a look at
?ppplotml instead.
Plot Densities
Use the plot, lines and points
generics to plot the densities.
hist(egypt$age, main = "Mortality in Ancient Egypt", freq = FALSE)
lines(mlweibull(egypt$age), lwd = 2, lty = 2, ylim = c(0, 0.025))
lines(mlgamma(egypt$age), lwd = 2, col = "red")
rug(egypt$age)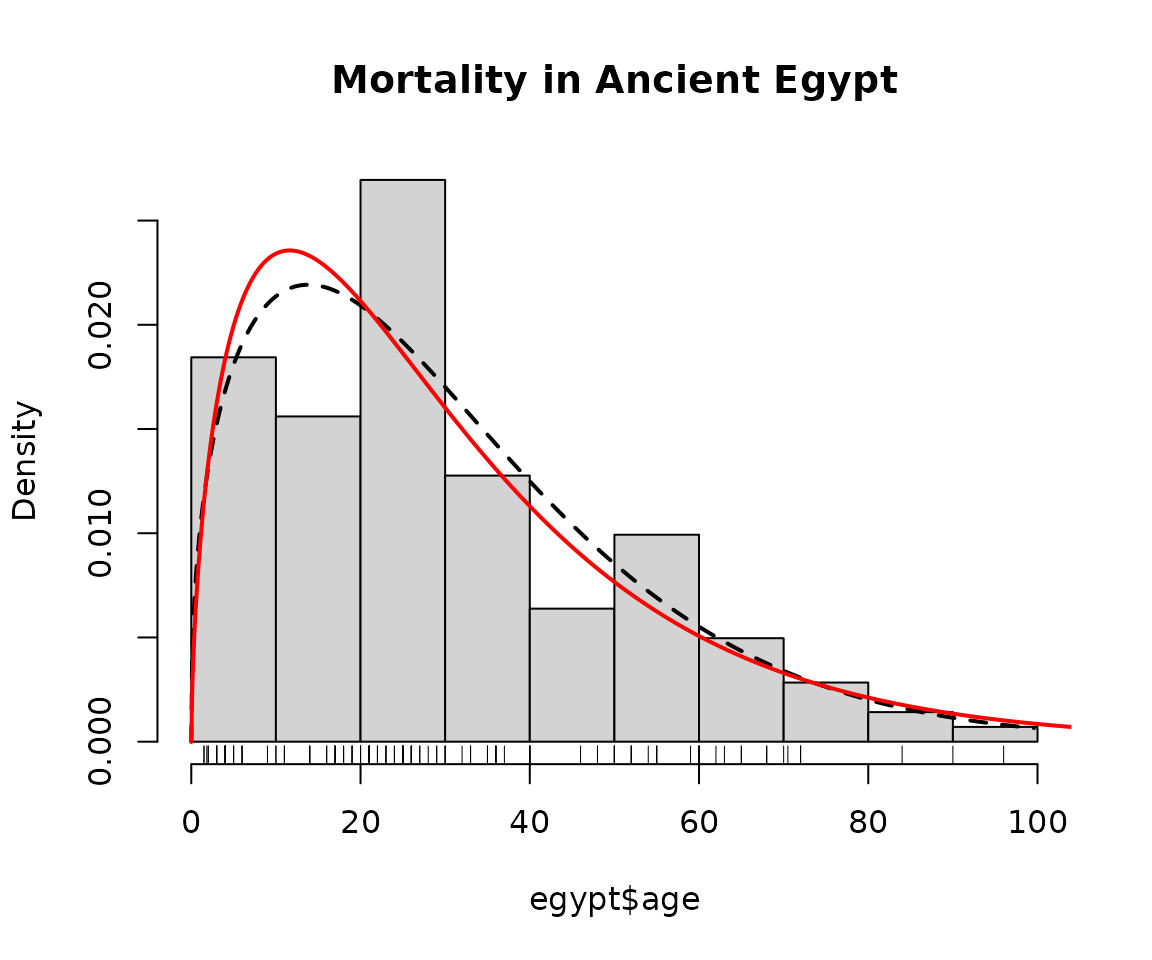
Confidence Intervals with Parametric Bootstrap
Now we want to get an idea about the uncertainties of our model
parameters. Do to this we can do a parametric bootstrap to calculate
confidence intervals using either bootstrapml or
confint. While bootstrapml allows you to
calculate any functional of the parameters and manipulate them
afterwards, confint is restricted to the main parameters of
the model.
# Calculate two-sided 95% confidence intervals for the two Gumbel parameters.
bootstrapml(mlweibull(egypt$age)) # same as confint(mlweibull(egypt$age))## 2.5% 97.5%
## shape 1.254423 1.605348
## scale 29.508024 37.593804
bootstrapml(mlgamma(egypt$age))## 2.5% 97.5%
## shape 1.33060624 2.03281195
## rate 0.04151886 0.06912931These confidence intervals are not directly comparable. That is, the
scale parameter in the Weibull model is not directly
comparable to the rate parameter in the gamma model. So let
us take a look at a a parameter with a familiar interpretation, namely
the mean.
The mean of the Weibull distribution with parameters
shape and scale is
scale*gamma(1 + 1/shape). On the other hand, the mean of
the Gamma distribution with parameters shape and
rate is shape/rate.
The probs argument can be used to modify the limits of
confidence interval. Now we will calculate two 90% confidence intervals
for the mean.
# Calculate two-sided 90% confidence intervals for the mean of a Weibull.
bootstrapml(mlweibull(egypt$age),
map = function(x) x[2] * gamma(1 + 1 / x[1]),
probs = c(0.05, 0.95)
)## 5% 95%
## 27.51011 33.73273
# Calculate two-sided 90% confidence intervals for the mean of a Gamma.
bootstrapml(mlgamma(egypt$age),
map = function(x) x[1] / x[2],
probs = c(0.05, 0.95)
)## 5% 95%
## 27.53893 34.11073We are be interested in the quantiles of the underlying distribution, for instance the median:
# Calculate two-sided 90% confidence intervals for the two Gumbel parameters.
bootstrapml(mlweibull(egypt$age),
map = function(x) qweibull(0.5, x[1], x[2]),
probs = c(0.05, 0.95)
)## 5% 95%
## 22.94823 28.81159
bootstrapml(mlgamma(egypt$age),
map = function(x) qgamma(0.5, x[1], x[2]),
probs = c(0.05, 0.95)
)## 5% 95%
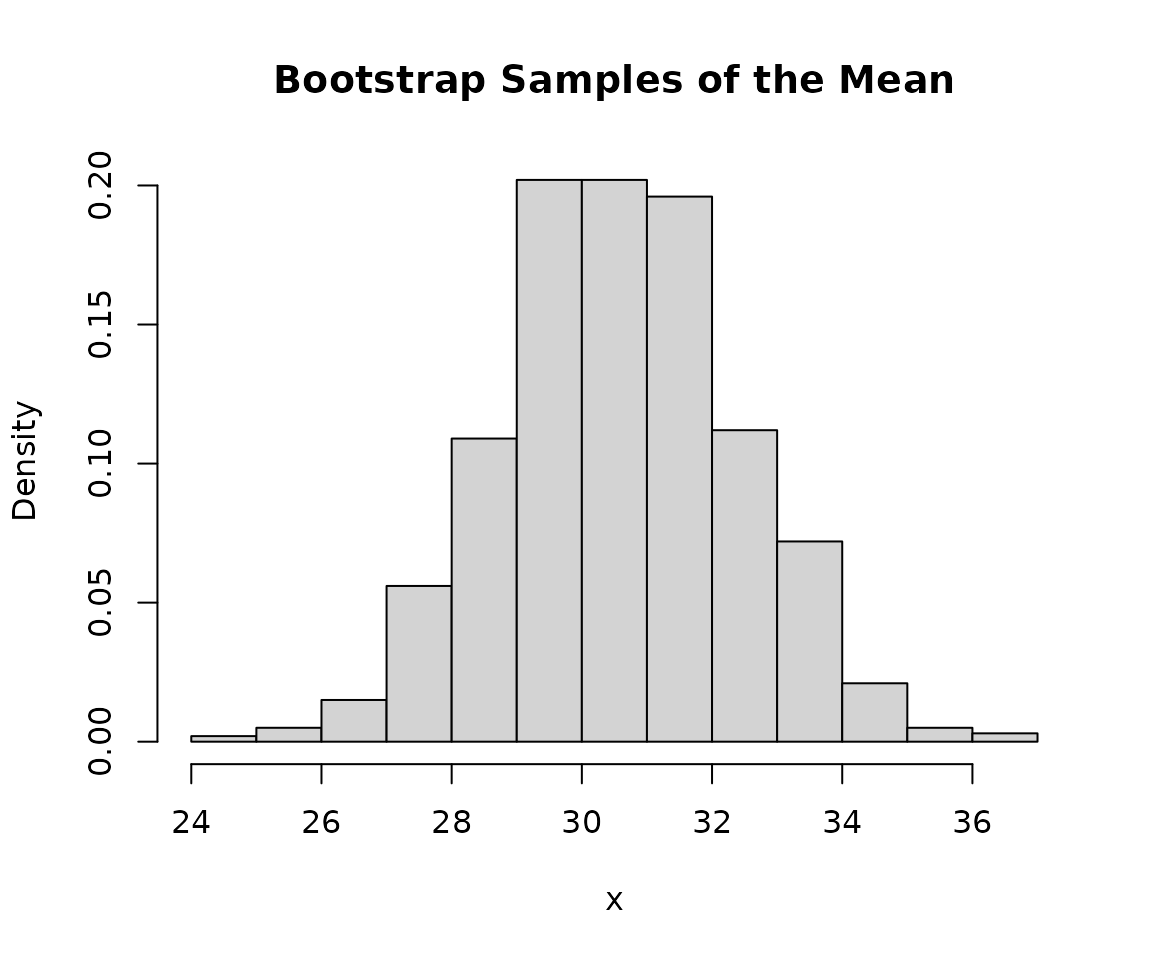
## 21.95519 27.63972We can also plot the bootstrap samples.
hist(
bootstrapml(mlweibull(egypt$age),
map = function(x) x[2] * gamma(1 + 1 / x[1]),
reducer = identity
),
main = "Bootstrap Samples of the Mean",
xlab = "x",
freq = FALSE
)
Density, CDF, quantiles and random variate generation
The functions dml, pml, qml
and rml can be used to calculate densities, cumulative
probabilities, quantiles, and generate random variables. Here are
random observations from the most likely distribution of Egyptian
mortalities given the Weibull model.
## [1] 25.90552 59.64456 13.36882 44.29378 12.22563 17.66144 54.57633 22.86824
## [9] 11.48328 19.94814Compare the empirical distribution of the random variates to the true cumulative probability.
set.seed(313)
obj <- mlweibull(egypt$age)
q <- seq(0, max(egypt$age), length.out = 100)
plot(q, pml(q, obj), type = "l", ylab = "Cumulative Probability")
r <- rml(100, obj)
lines(ecdf(r))
